-
스도쿠 푸는 요령의 핵심은 두 가지 기본 규칙을 이해하는 것입니다. 가로줄과 세로줄, 그리고 3x3 작은 사각형 각각에 1부터 9까지의 숫자가 단 한 번씩만 들어가야 한다는 원칙입니다. 이 규칙을 바탕으로 빈칸에 들어갈 수 있는 유일한 숫자를 논리적으로 찾아내는 것이 문제 해결의 첫걸음입니다.
스도쿠 푸는 요령
효과적인 스도쿠 푸는 요령의 첫 단계는 가장 기본적인 규칙을 완벽히 이해하는 것입니다. 바로 가로줄, 세로줄, 그리고 3x3 크기의 작은 사각형 안에는 1부터 9까지의 숫자가 절대로 겹치지 않게 들어가야 한다는 점입니다.
이 간단한 원칙을 어떻게 적용하고 확장하느냐에 따라 문제의 난이도가 결정됩니다. 처음에는 이 규칙을 계속 되뇌면서 빈칸을 채워나가는 연습을 하는 것이 좋습니다.
가장 먼저 시도해 볼 수 있는 방법은 거의 다 채워진 부분을 공략하는 것입니다. 예를 들어, 9개의 칸으로 구성된 작은 사각형이나 가로, 세로줄에서 단 하나의 숫자만 비어있는 경우를 찾아보는 것이죠.
이때는 고민할 필요 없이 1부터 9까지의 숫자 중 그곳에 빠진 유일한 숫자를 찾아 채워 넣으면 됩니다. 이는 가장 확실하고 빠른 해결책 중 하나입니다.

조금 더 나아가면 '소거법'을 활용할 수 있습니다. 특정 빈칸에 들어갈 숫자를 찾아야 할 때, 그 칸이 포함된 가로줄, 세로줄, 그리고 3x3 사각형에 이미 있는 숫자들을 모두 제외하는 방식입니다.
예를 들어, 어떤 칸의 가로줄에 '1, 3, 5'가 있고 세로줄에 '2, 6'이 있다면, 그 칸에는 이 숫자들은 들어갈 수 없다는 것을 알 수 있습니다. 이렇게 후보 숫자를 줄여나가다 보면 정답이 보이기 시작합니다.
특정 숫자에 집중하는 것도 좋은 전략입니다. 예를 들어, 숫자 '7'을 아직 채우지 못한 3x3 사각형이 있다고 가정해 봅시다. 이때 다른 가로줄과 세로줄에 있는 '7'의 위치를 확인하면, 해당 사각형에서 '7'이 들어갈 수 없는 위치들을 파악할 수 있습니다.
이 과정을 통해 결국 '7'이 들어갈 수 있는 유일한 후보 칸이 남게 되는데, 이것이 바로 정답의 위치입니다. 이 방법은 중급 난이도에서 매우 유용하게 사용됩니다.

문제가 복잡해지면 빈칸에 들어갈 수 있는 후보 숫자들을 작게 메모하는 것이 큰 도움이 됩니다. 소거법을 통해 각 빈칸에 들어갈 가능성이 있는 숫자들을 모두 적어두는 것입니다.
이렇게 후보를 모두 적어두면, 어떤 칸에 특정 숫자가 확정되는 순간 그 숫자가 포함된 가로줄, 세로줄, 3x3 사각형 내의 다른 후보 숫자들에서 해당 숫자를 지울 수 있습니다. 이 과정이 연쇄적으로 일어나며 문제가 풀리게 됩니다.
만약 풀이 과정이 막혔다면, 잠시 쉬거나 처음부터 다시 검토하는 것이 좋습니다. 특히 하나의 숫자를 잘못 입력하면 모든 논리가 엉켜버리기 때문에, 이전에 찾았던 숫자들이 규칙에 맞게 잘 배치되었는지 확인하는 과정은 매우 중요합니다.
때로는 미처 발견하지 못했던 아주 쉬운 단서가 숨어있을 수도 있습니다. 조급해하지 않고 차분하게 전체 판을 다시 살펴보는 여유를 가지는 것이 중요합니다.
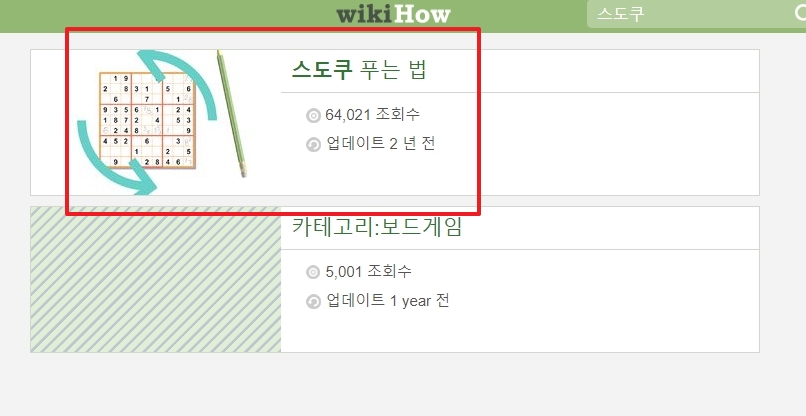
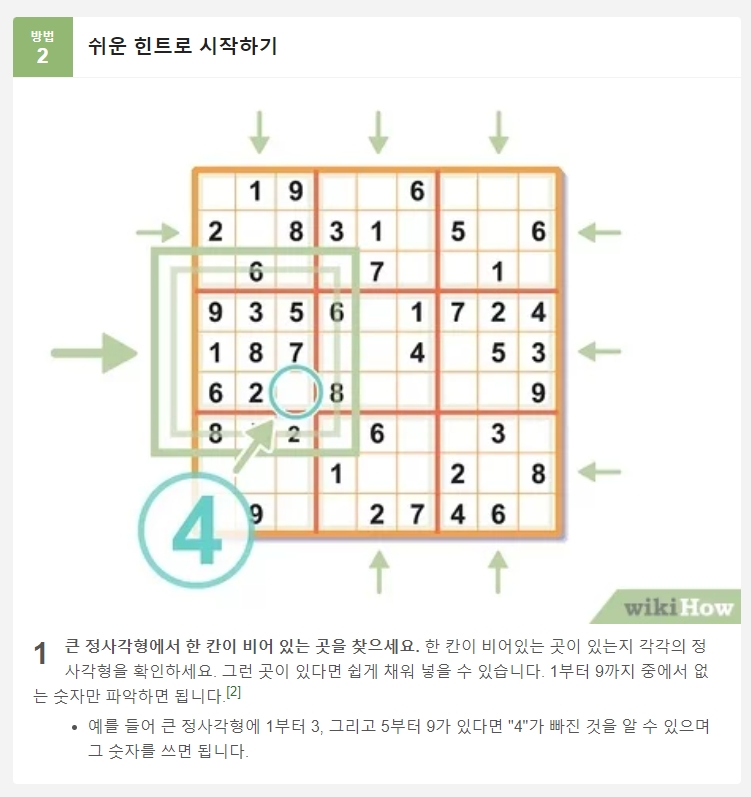
이 그림은 가장 기본적인 전략을 잘 보여줍니다. 왼쪽 위의 3x3 사각형을 보면 1부터 9까지의 숫자 중 '4'만 빠져있는 것을 한눈에 알 수 있습니다. 다른 줄을 살펴볼 필요도 없이 빈칸의 정답은 '4'가 됩니다.
스도쿠를 시작할 때 가장 먼저 해야 할 일은 이처럼 8개의 숫자가 이미 채워진 사각형이나 줄이 있는지 찾아보는 것입니다. 이것이 가장 확실한 출발점입니다.
이제 규칙을 조금 더 복합적으로 적용해 보겠습니다. 특정 빈칸을 중심으로, 그 칸이 속한 가로줄과 세로줄에 어떤 숫자들이 있는지 모두 확인합니다. 그러면 그 줄에 이미 있는 숫자들은 해당 빈칸에 들어갈 수 없습니다.
여기에 3x3 사각형 규칙까지 더해 후보 숫자를 지워나가다 보면, 단 하나의 숫자만 남는 경우가 있습니다. 이 숫자가 바로 그 칸의 정답이 되는 원리입니다.
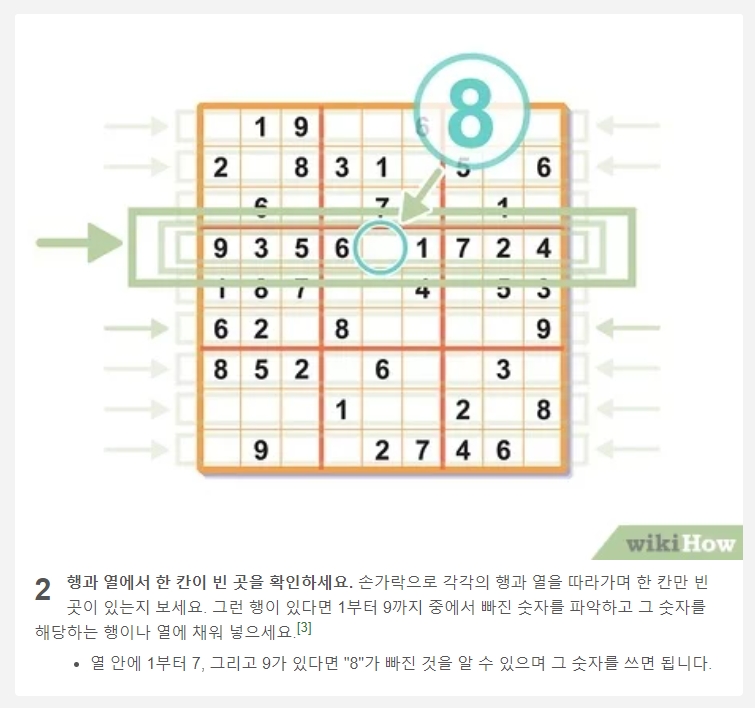
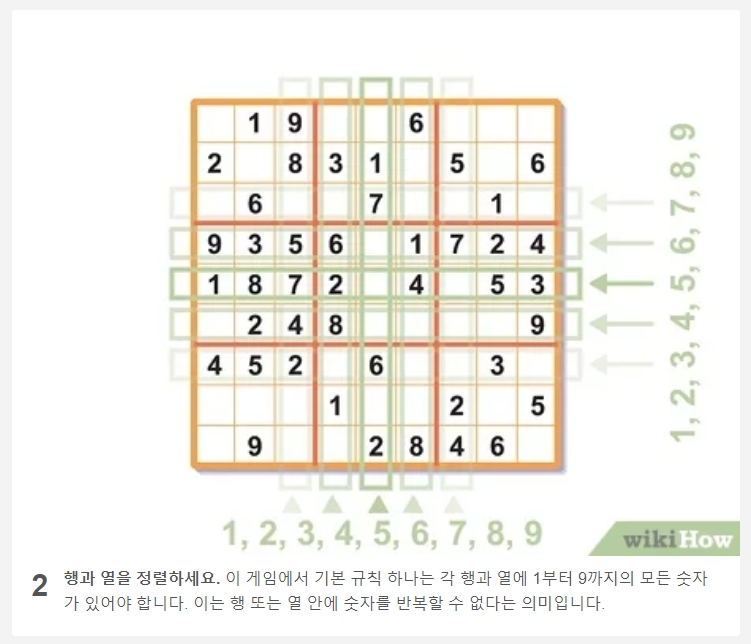
이 그림은 소거법의 좋은 예시입니다. 중앙 상단 3x3 사각형의 빈칸에 주목해 보세요. 해당 칸의 세로줄에는 이미 '8'이 있고, 다른 가로줄에도 '8'이 존재하여 다른 칸들을 막고 있습니다.
결과적으로, 이 3x3 사각형 안에서 '8'이 들어갈 수 있는 유일한 자리는 바로 표시된 저곳뿐입니다. 이처럼 주변의 숫자들을 단서로 활용하여 정답을 찾아내는 것이 스도쿠의 묘미입니다.
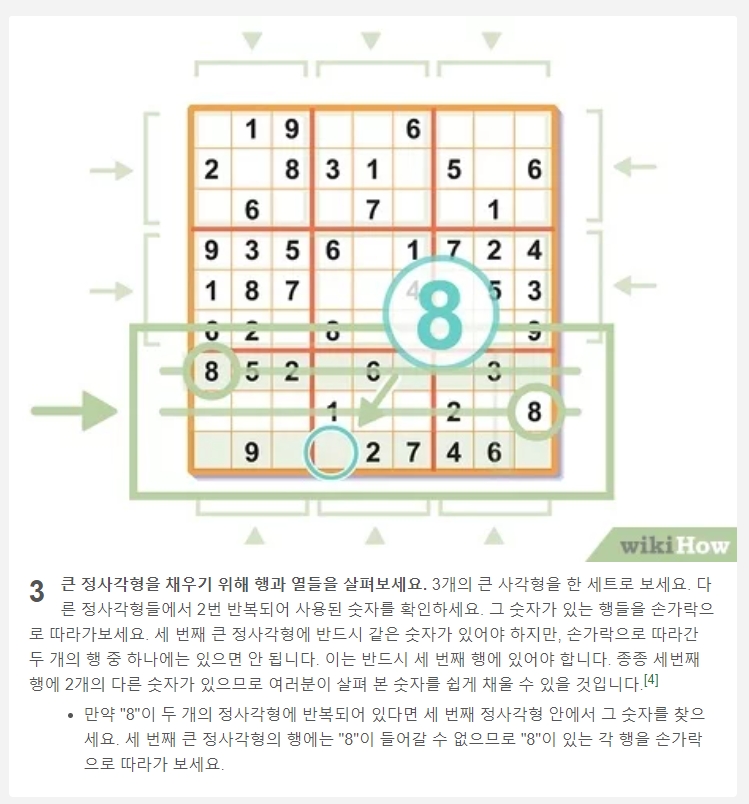
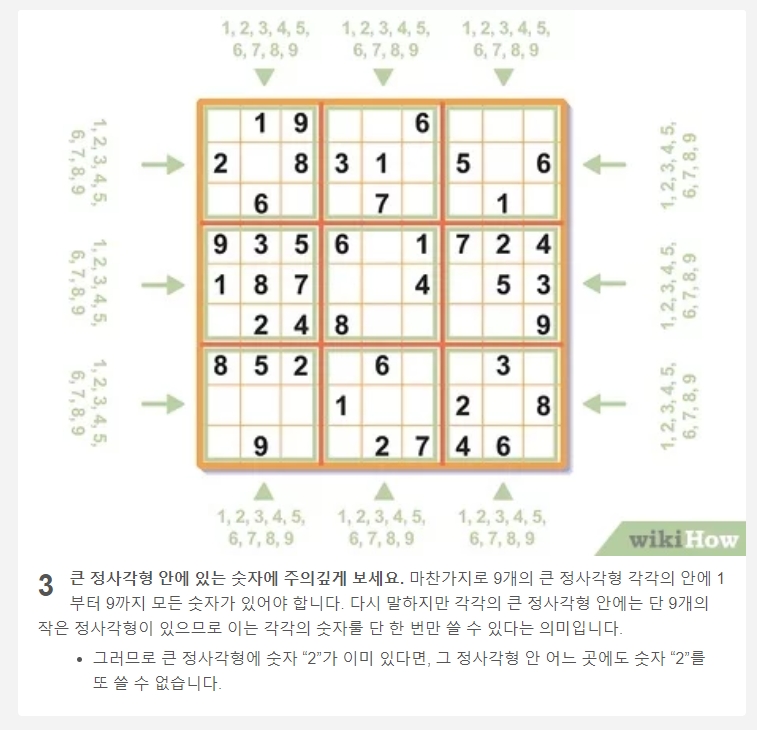
하나의 숫자를 따라가는 전략은 매우 효과적입니다. 예를 들어, 전체 퍼즐에서 숫자 '7'의 배치를 살펴보는 것입니다. 이미 배치된 '7'들이 차지한 가로줄과 세로줄을 모두 제외하면, '7'이 아직 없는 3x3 사각형에서 들어갈 수 있는 위치가 크게 제한됩니다.
이 그림처럼, 다른 줄에 있는 '7'들 때문에 오른쪽 위 사각형에서는 표시된 한 곳에만 '7'이 들어갈 수 있게 됩니다. 이 방식을 1부터 9까지 모든 숫자에 적용해 볼 수 있습니다.
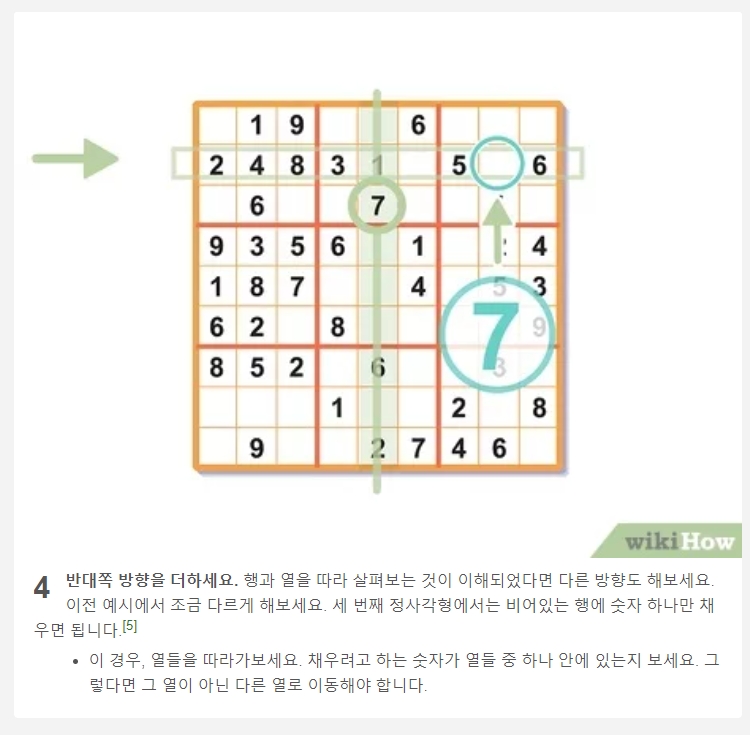
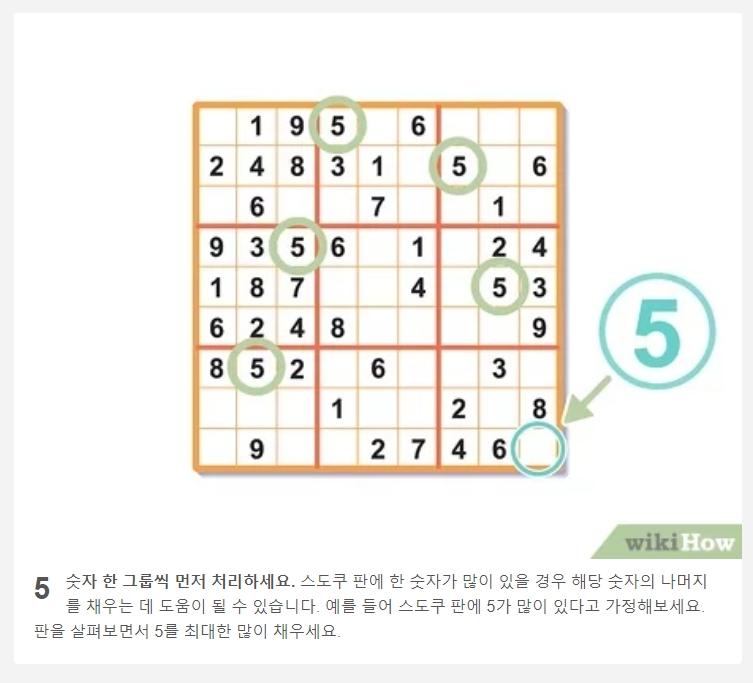
이 방법은 여러 단계를 거쳐야 하는 조금 더 발전된 전략입니다. 먼저, 두 개의 다른 3x3 사각형에 있는 숫자 '5'의 위치를 확인합니다. 이 두 개의 '5'가 각각 특정 가로줄과 세로줄을 차지하게 됩니다.
이 정보를 종합하면, 아직 '5'가 없는 남은 사각형(오른쪽 아래)에서 '5'가 들어갈 수 있는 유일한 자리가 결정됩니다. 여러 정보를 조합하여 논리적으로 결론을 도출하는 것이 바로 고난도 스도쿠 풀이의 핵심입니다.
댓글